Isogeometric Analysis: B-spline Curves and Surfaces in Octave and TypeScript

In the previous blog post here I implemented Bézier curves. There are other important structures that are used in computer graphics and I’d need those structures to define a domain and a solution in IGA for my implementation here: https://github.com/carlonluca/isogeometric-analysis.
Bézier curves are great, but the polynomials needed to describe some curves may need a high degree to satisfy multiple constraints. To overcome this problem, some structures were designed to use piecewise-polynomials instead. Examples in this case are NURBS and B-splines.
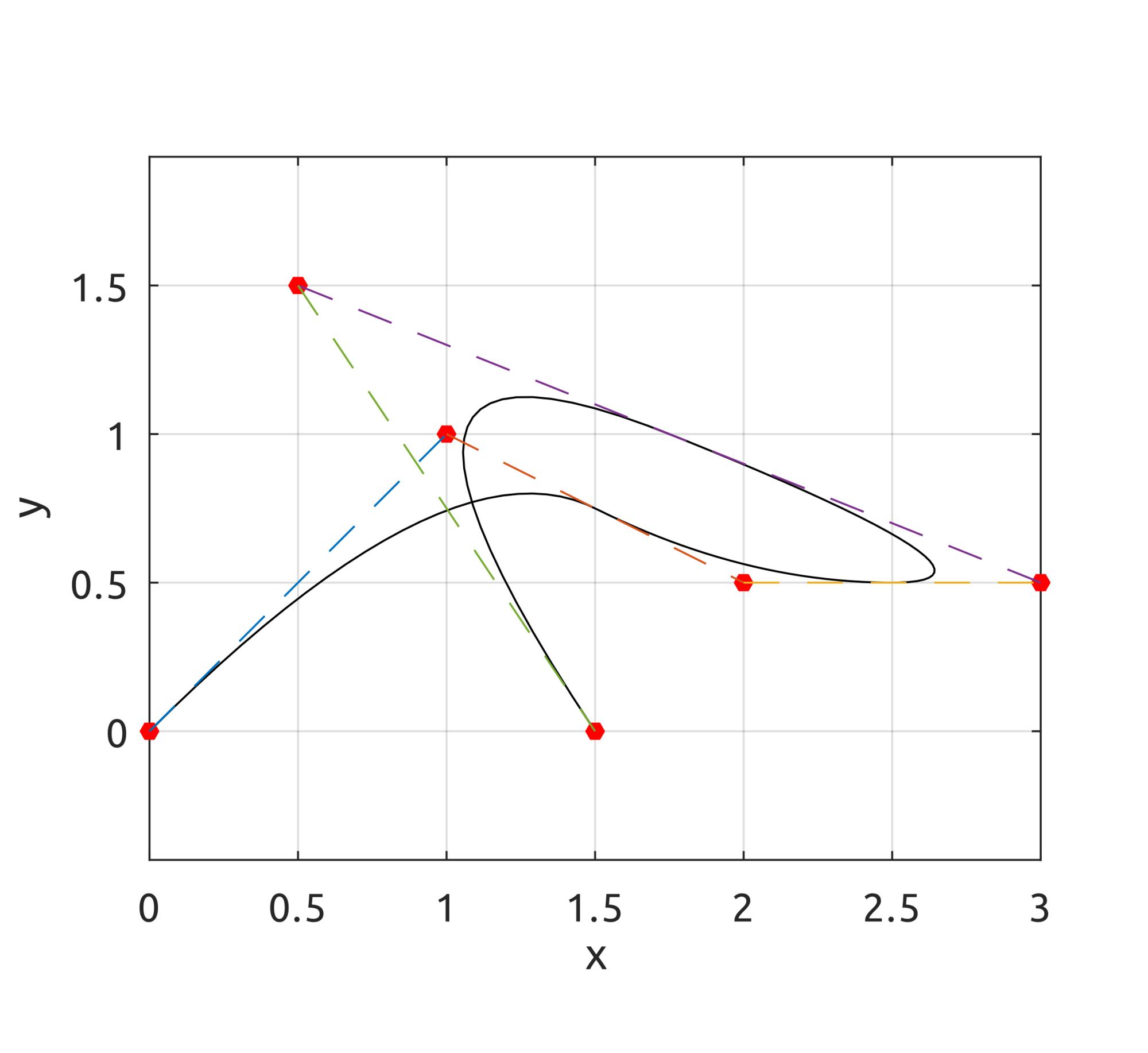
 The drawBsplineCurve script draws, instead, the real curve. For example, to draw the B-spline of degree $p=2$ defined over the knot vector $Xi=[0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1]$ with control points:
The drawBsplineCurve script draws, instead, the real curve. For example, to draw the B-spline of degree $p=2$ defined over the knot vector $Xi=[0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1]$ with control points:
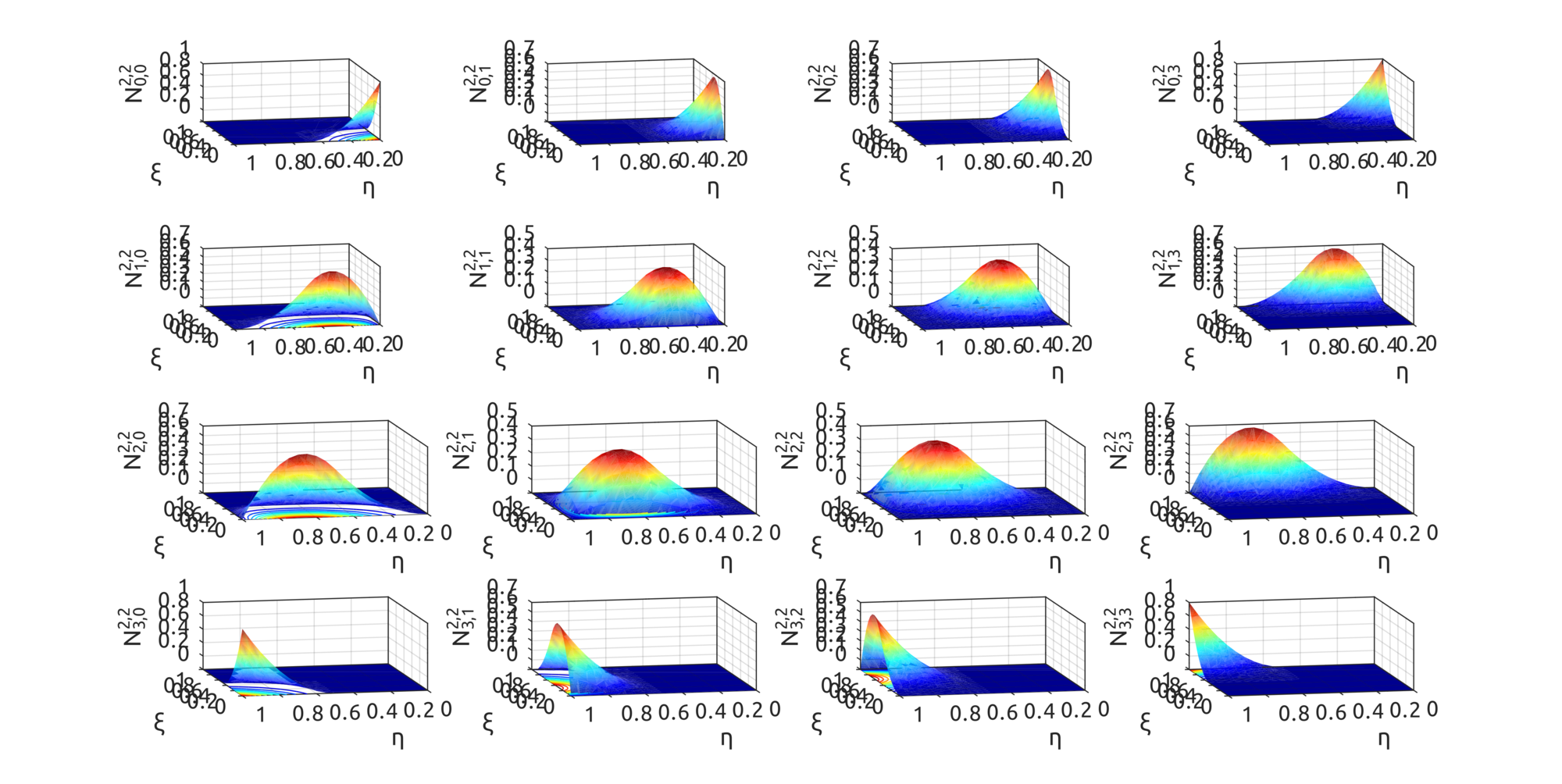
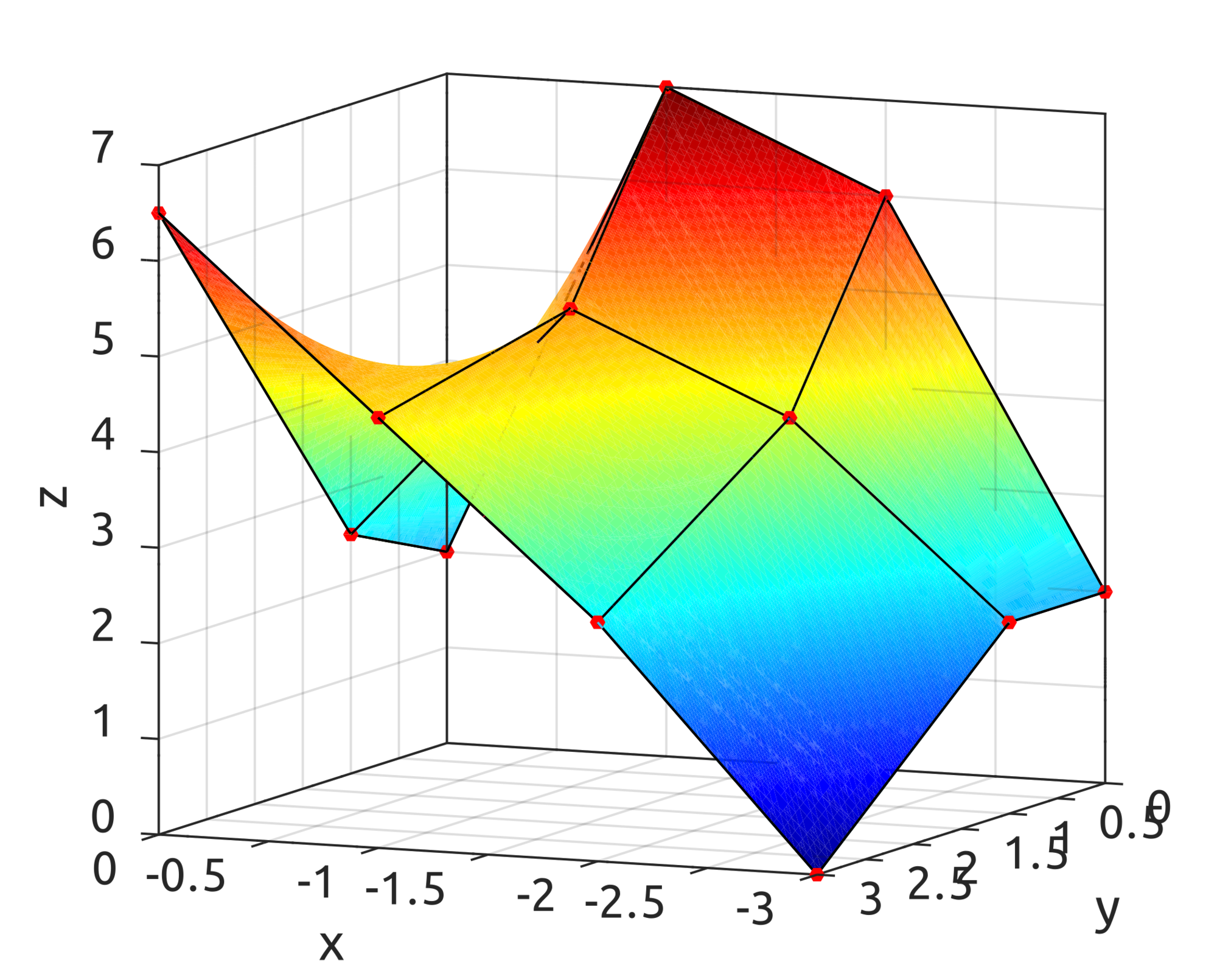
 For surfaces, drawBivariateBsplineBasisFuns can be used to draw bivariate basis functions. For example:
For surfaces, drawBivariateBsplineBasisFuns can be used to draw bivariate basis functions. For example:
 By using the defined basis functions, data defined in https://github.com/carlonluca/isogeometric-analysis/blob/master/3.4/defineBsplineRing.m can draw a shape similar to a ring:
By using the defined basis functions, data defined in https://github.com/carlonluca/isogeometric-analysis/blob/master/3.4/defineBsplineRing.m can draw a shape similar to a ring:
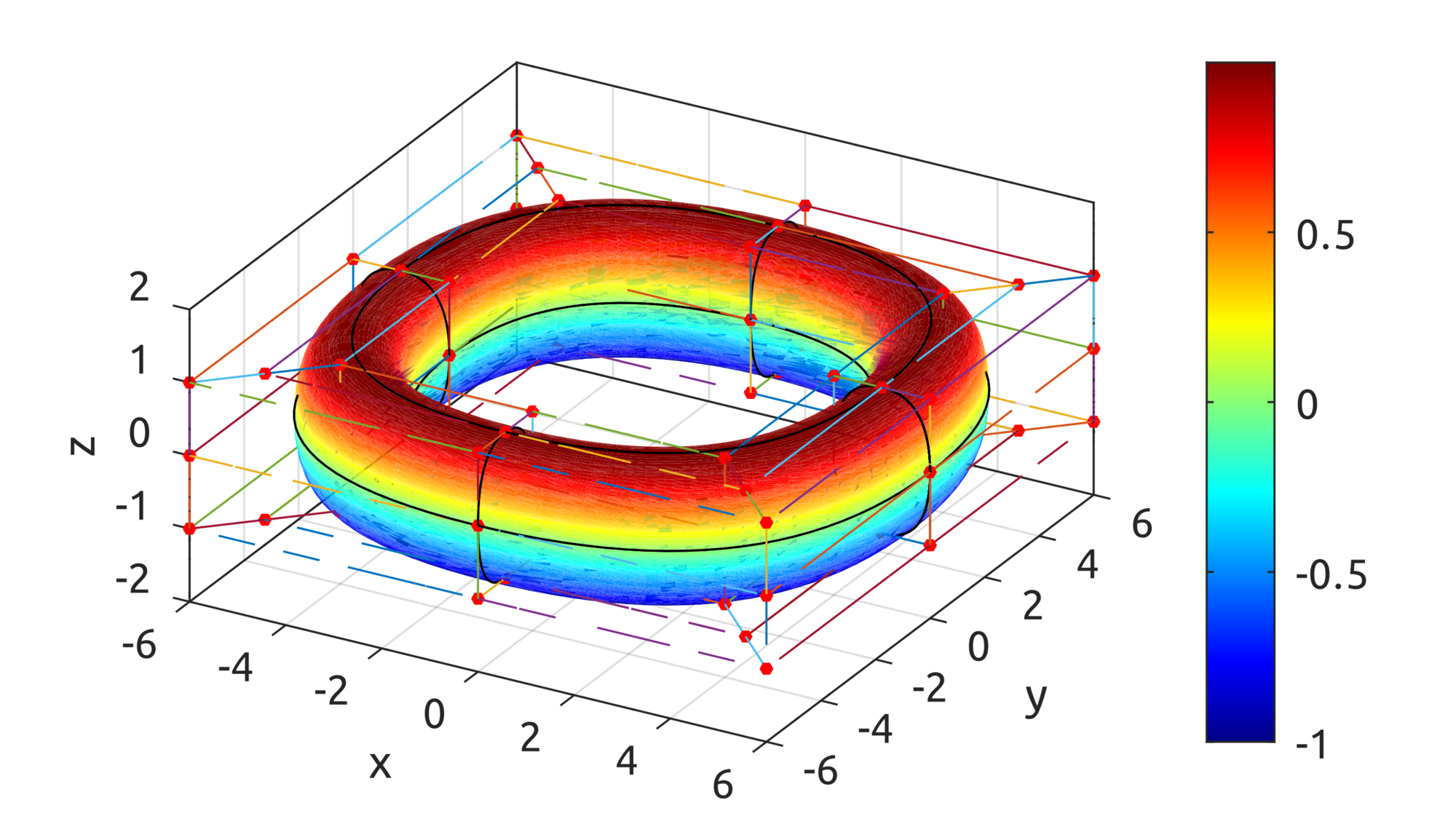 Note that this is not yet a toroid.
As you can see below, you can define surfaces and decide for the degree of the polynomials to use for each direction:
Note that this is not yet a toroid.
As you can see below, you can define surfaces and decide for the degree of the polynomials to use for each direction:
 By using points with 3 coordinates a curve in 3 dimensions can be drawn:
and we can also observe the B-spline basis functions being used in the calculation:
For surfaces, the BsplineSurf can draw the surface with the equations above. This is an example with degree 1 in one direction:
this is an example with degree 2:
Plots are drawn using Plotly, but the implementation is pure TypeScript.
By using points with 3 coordinates a curve in 3 dimensions can be drawn:
and we can also observe the B-spline basis functions being used in the calculation:
For surfaces, the BsplineSurf can draw the surface with the equations above. This is an example with degree 1 in one direction:
this is an example with degree 2:
Plots are drawn using Plotly, but the implementation is pure TypeScript.
B-spline Curves
B-splines are curves that are described using piecewise-polynomials with minimal support. The parametric domain is split into multiple ranges by using a vector. The general definition of a B-spline curve is:
$$\displaylines{\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\\
a\leq\xi\leq b}$$
where $\boldsymbol{P}_{i}$’s are the control points of the curve and the functions $N_{i}^{p}left(xiright)$ are basis functions defined as:
$$\displaylines{N_{i}^{0}\left(\xi\right)=\left\{ \begin{array}{ll}1, & \xi_{i}\leq\xi<\xi_{i+1}\\0,&\text{otherwise}\end{array}\right.,\\
N_{i}^{p}\left(\xi\right)=\frac{\xi-\xi_{i}}{\xi_{i+p}-\xi_{i}}\cdot N_{i}^{p-1}\left(\xi\right)+\frac{\xi_{i+p+1}-\xi}{\xi_{i+p+1}-\xi_{i+1}}\cdot N_{i+1}^{p-1}\left(\xi\right),\\
a\leq\xi\leq b}$$
The values $\xi_{i}$ are elements of the aforementioned knot vector, defined as:
$$\displaylines{\Xi=\left[\underset{p+1}{\underbrace{a,\ldots,a}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b,\ldots,b}}\right],\\
\left|\Xi\right|=n+p+2}$$
where $p$ is the degree of the basis functions. A knot vector in this form is said to be nonperiodic or clamped or open.
B-spline Surfaces
By using the tensor product we can obtain B-splines in spaces of higher dimension. For surfaces, given the knot vectors:
$$\displaylines{\Xi=\left[\underset{p+1}{\underbrace{a_{0},\ldots,a_{0}}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b_{0},\ldots,b_{0}}}\right],\\
\left|\Xi\right|=n+p+2\\
H=\left[\underset{q+1}{\underbrace{a_{1},\ldots,a_{1}}},\xi_{q+1},\ldots,\xi_{m},\underset{q+1}{\underbrace{b_{1},\ldots,b_{1}}}\right],\\
\left|H\right|=m+q+2}$$
a B-spline surface can be defined as:
$$\displaylines{\boldsymbol{S}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)\boldsymbol{P}_{i,j},\\
\left\{ \begin{array}{c}
a_{0}\leq\xi\leq b_{0}\\
a_{1}\leq\eta\leq b_{1}
\end{array}\right.}$$
where $p$ and $q$ are the degrees of the polynomials. In the implementations, sometimes I preferred the matrix form of the equations:
$$\displaylines{\boldsymbol{C}\left(\xi\right)=\left[N_{i-p}\left(\xi\right),\ldots,N_{i}\left(\xi\right)\right]\cdot\left[\begin{array}{c}
\boldsymbol{P}_{i-p}\\
\vdots\\
\boldsymbol{P}_{i}
\end{array}\right],\\
\xi\in\left[\xi_{i},\xi_{i+1}\right)}$$
For the surfaces instead, the matrix form is:
$$\displaylines{\boldsymbol{S}\left(\xi,\eta\right)=\left[N_{i-p}\left(\xi\right),\ldots,N_{i}\left(\xi\right)\right]\cdot\left[\begin{array}{ccc}
\boldsymbol{P}_{j-q,i-p} & \cdots & \boldsymbol{P}_{j-q,i}\\
\vdots & \ddots & \vdots\\
\boldsymbol{P}_{j,i-p} & \cdots & \boldsymbol{P}_{j,i}
\end{array}\right]\cdot\left[\begin{array}{c}
N_{j-q}\left(\eta\right)\\
\vdots\\
N_{j}\left(\eta\right)
\end{array}\right],\\
\xi\in\left[\xi_{i},\xi_{i+1}\right),\eta\in\left[\eta_{j},\eta_{j+1}\right)}$$
These forms leverage a more performant algorithm for the computation of the basis functions, which returns the value of all nonvanishing functions for a point in the parametric space. The Octave implementation is clearly simpler as Octave has native support for matrices, the TypeScript implementation instead includes a basic Matrix2 class that offers the simplest operators.
Octave Implementation
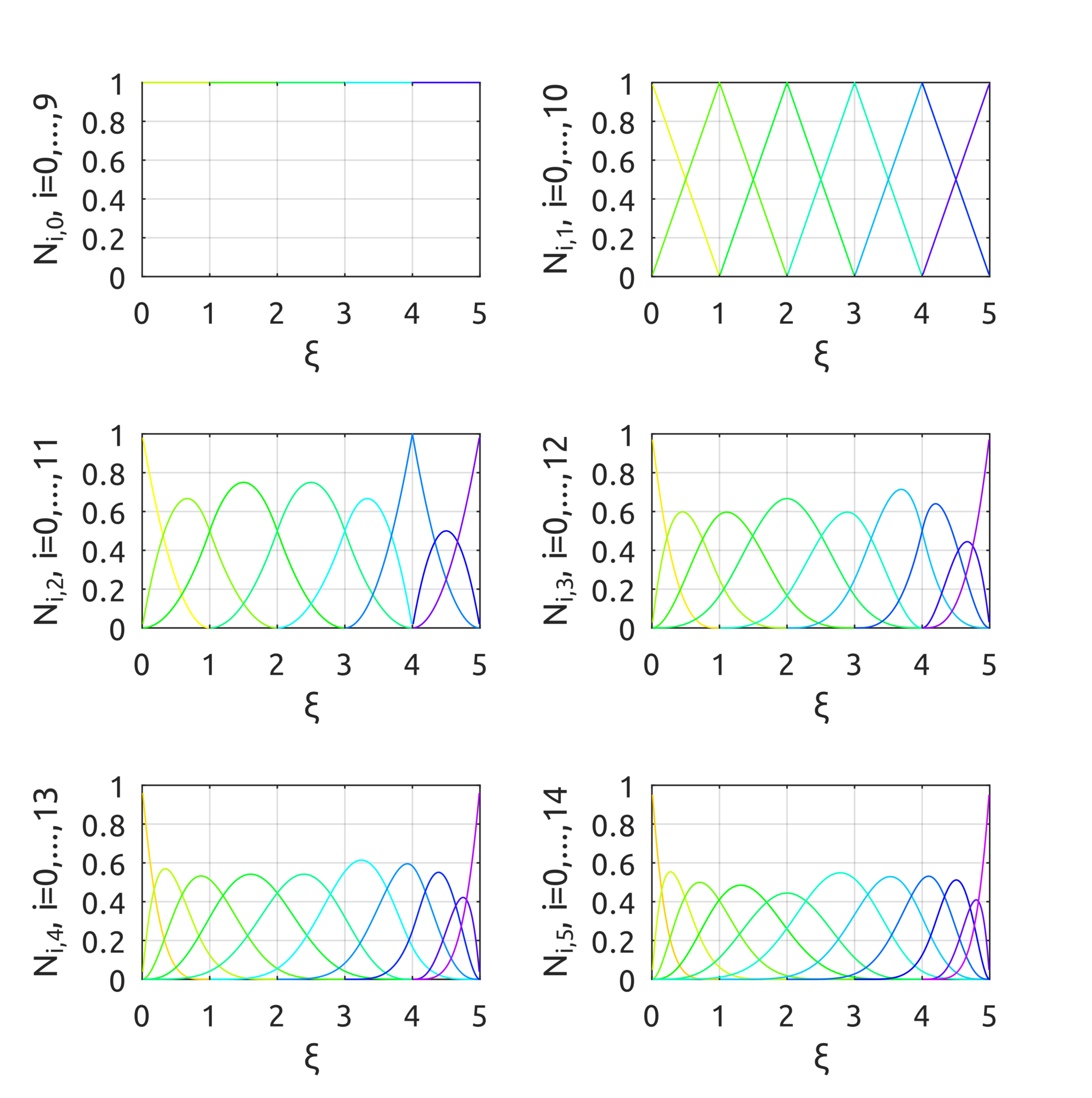
An implementation for Octave is provided in https://github.com/carlonluca/isogeometric-analysis/tree/master/3.4. There are examples to show how to draw B-spline curves with the implementation. For example, the drawBsplineBasisFuns script shows the B-spline basis functions over the knot vector $Xi=[0, 0, 0, 1, 2, 3, 4, 4, 5, 5, 5]$ using the provided implementation of the basis functions:
$$\displaylines{\boldsymbol{P}_{0}=\left(0,0,0\right),\;\boldsymbol{P}_{1}=\left(1,1,1\right),\;\boldsymbol{P}_{2}=\left(2,0.5,0\right)\\
\boldsymbol{P}_{3}=\left(3,0.5,0\right),\;\boldsymbol{P}_{4}=\left(0.5,1.5,0\right),\;\boldsymbol{P}_{5}=\left(1.5,0,1\right)}$$
a simple call to:
drawBsplineCurve(5, 2, [
0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1
], [
0, 0; 1, 1; 2, 0.5; 3, 0.5; 0.5, 1.5; 1.5, 0
]);
draws:

drawBivariateBsplineBasisFuns([
0, 0, 0, 0.5, 1, 1, 1
], 3, 2, [
0, 0, 0, 0.5, 1, 1, 1
], 3, 2);
gives this result:




TypeScript Implementation
A TypeScript implementation is also present in the repo. With a simple code like this:let controlPoints = [] controlPoints.push(new Point(0, 0)) controlPoints.push(new Point(1, 1)) controlPoints.push(new Point(2, 0.5)) controlPoints.push(new Point(3, 0.5)) controlPoints.push(new Point(0.5, 1.5)) controlPoints.push(new Point(1.5, 0)) let knotVector = [ 0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1 ] drawBsplineCurve(controlPoints, knotVector, 2, false, drawControlPoints, plot, bernsteinPlot)It is possible to draw the B-spline curve in a div: