Isogeometric Analysis: NURBS curves and surfaces in Octave and TypeScript
In this blog post I wrote some notes about B-splines. There are however important classes of curves and surfaces that cannot be represented by piecewise-polynomials like circles, ellipses etc… NURBS come to the rescue.
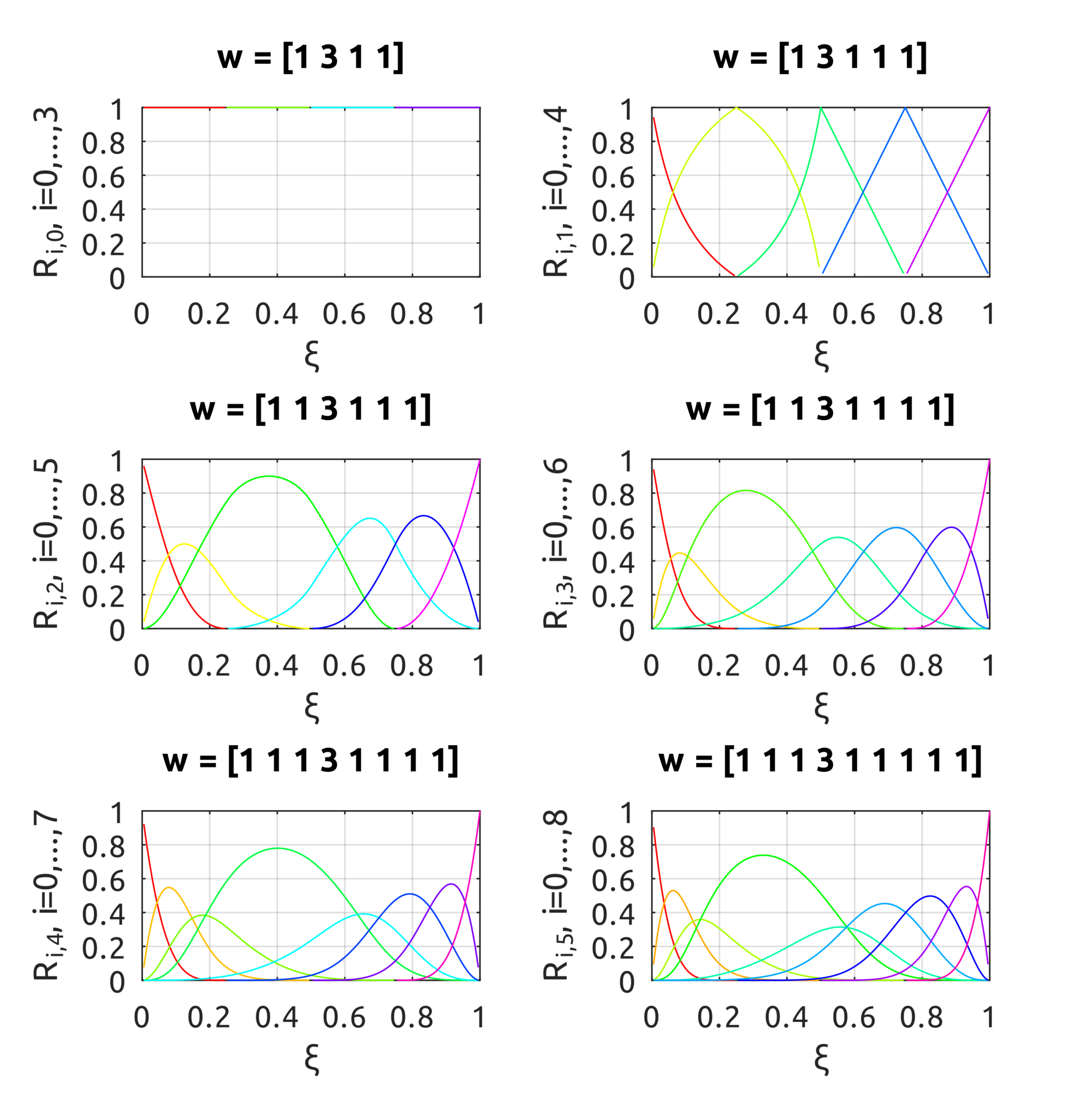in the plots the effect of the weight is pretty clear. From top to bottom, the degree of the basis funs is increased over the knot vector $\Xi = [0.25, 0.5, 0.75]$.
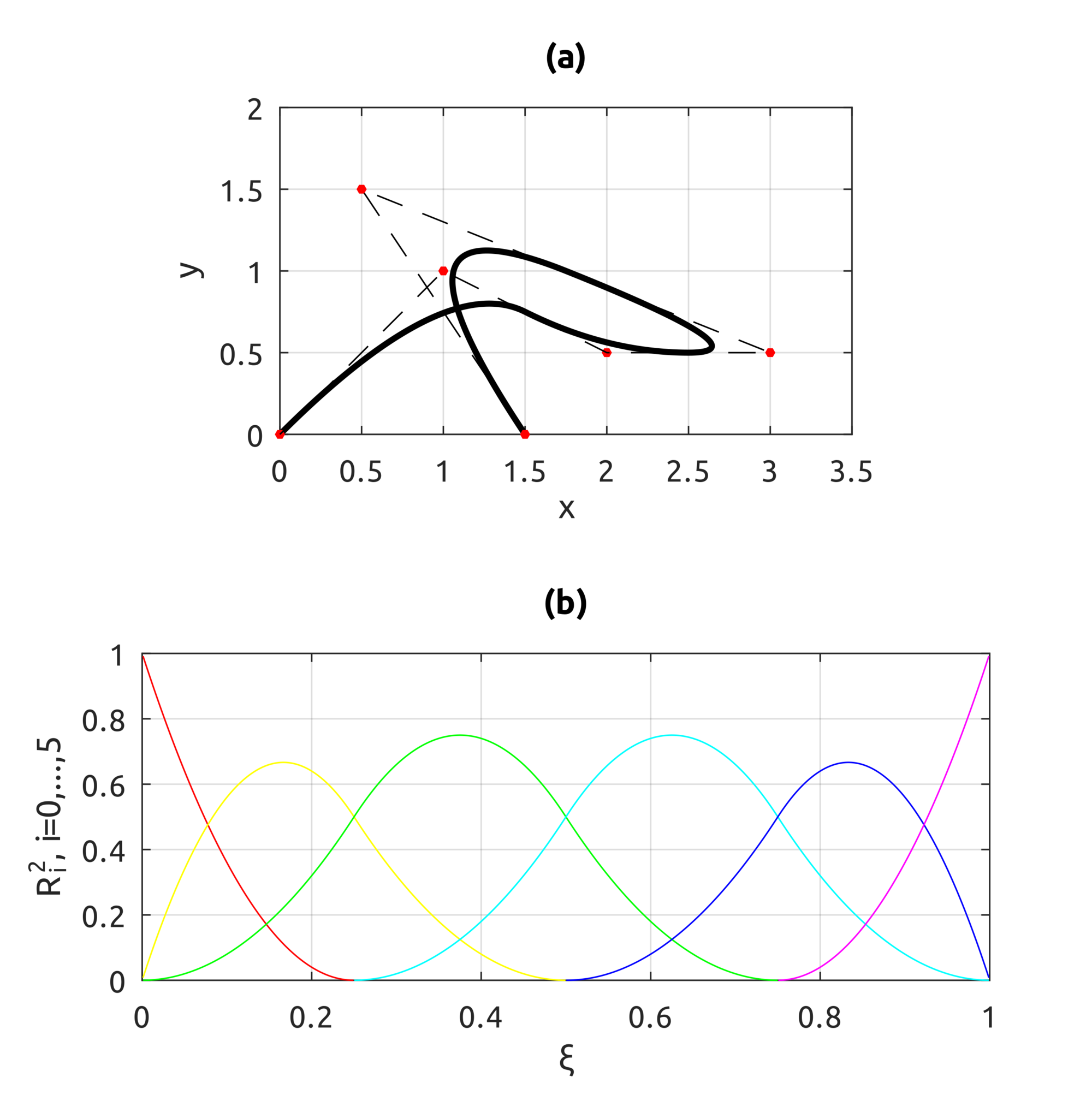
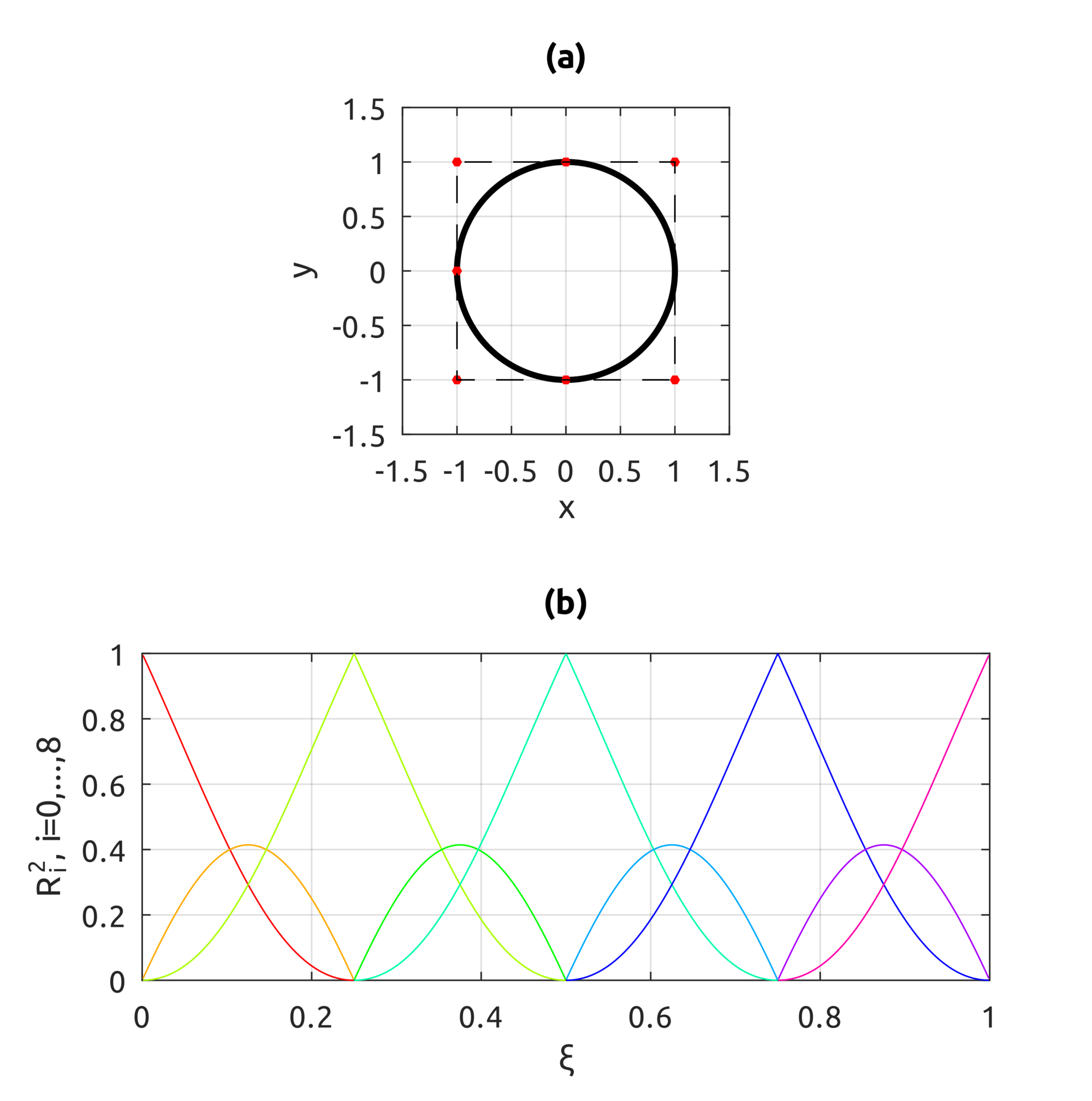
The computeNURBSCurvePoint script uses homogeneous coords to compute a NURBS curve using B-spline basis functions. We can build curves similar to what we could draw with B-splines but we can also draw circles:
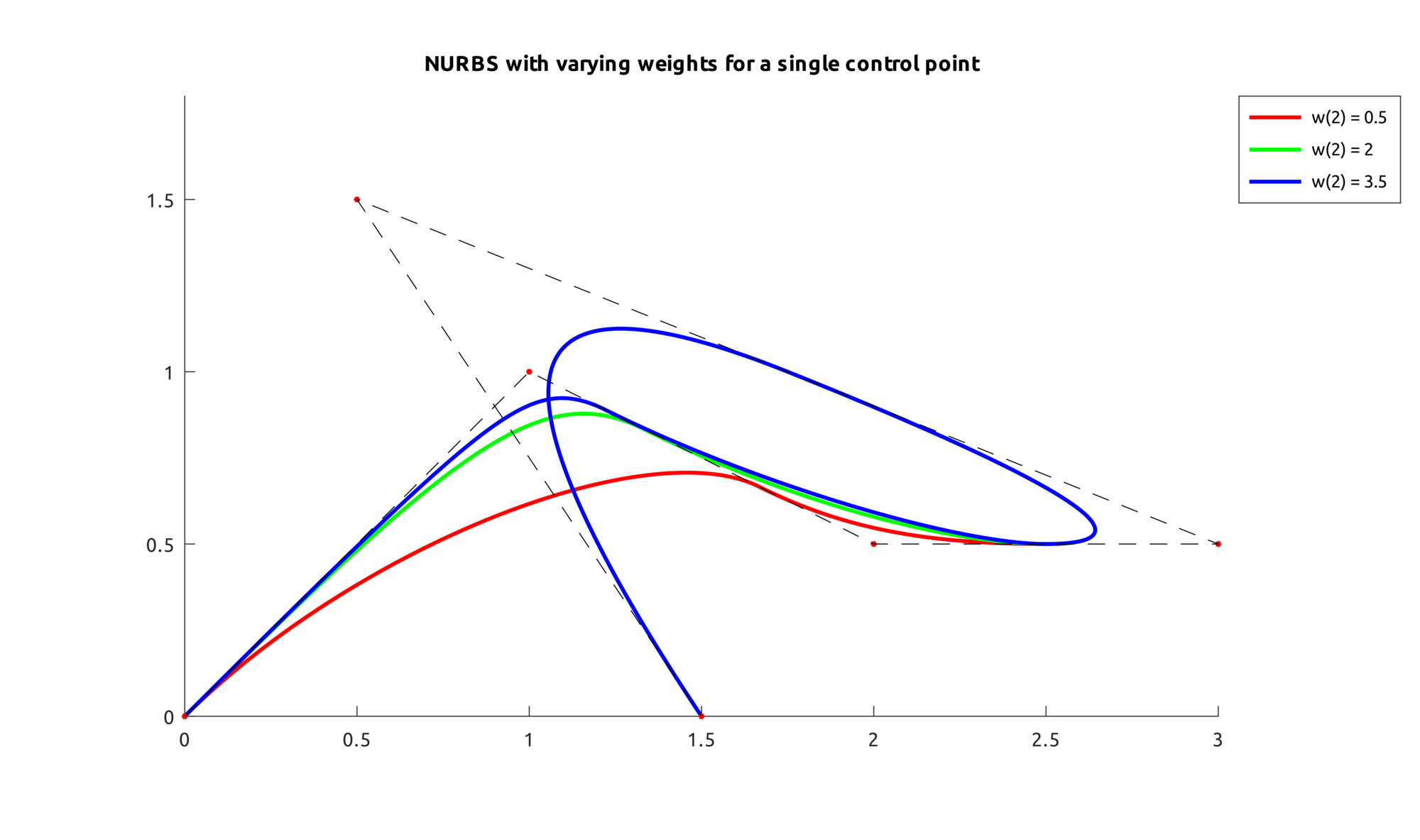
This is an example that shows what happens when a weight is increased on one point:
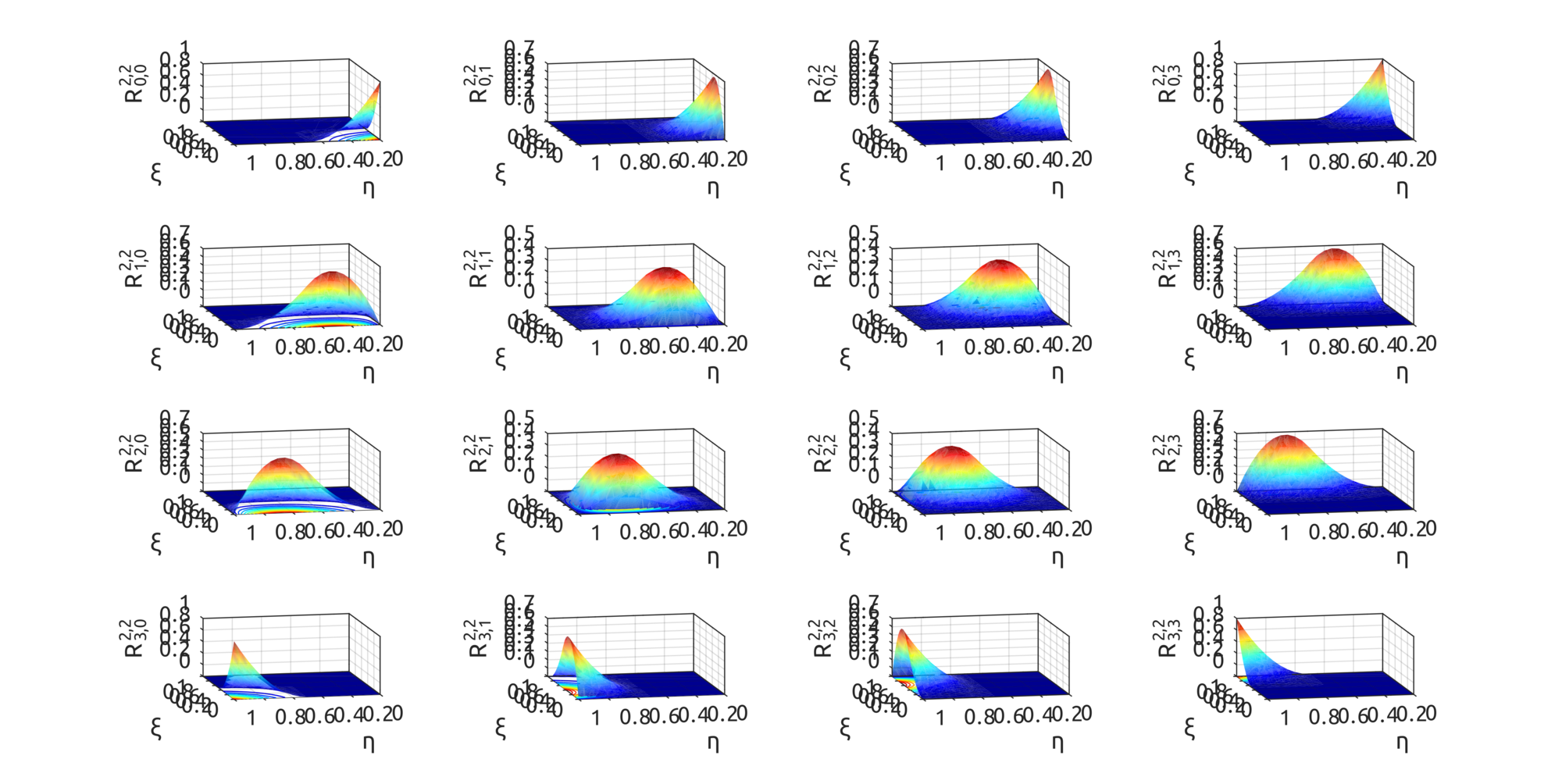
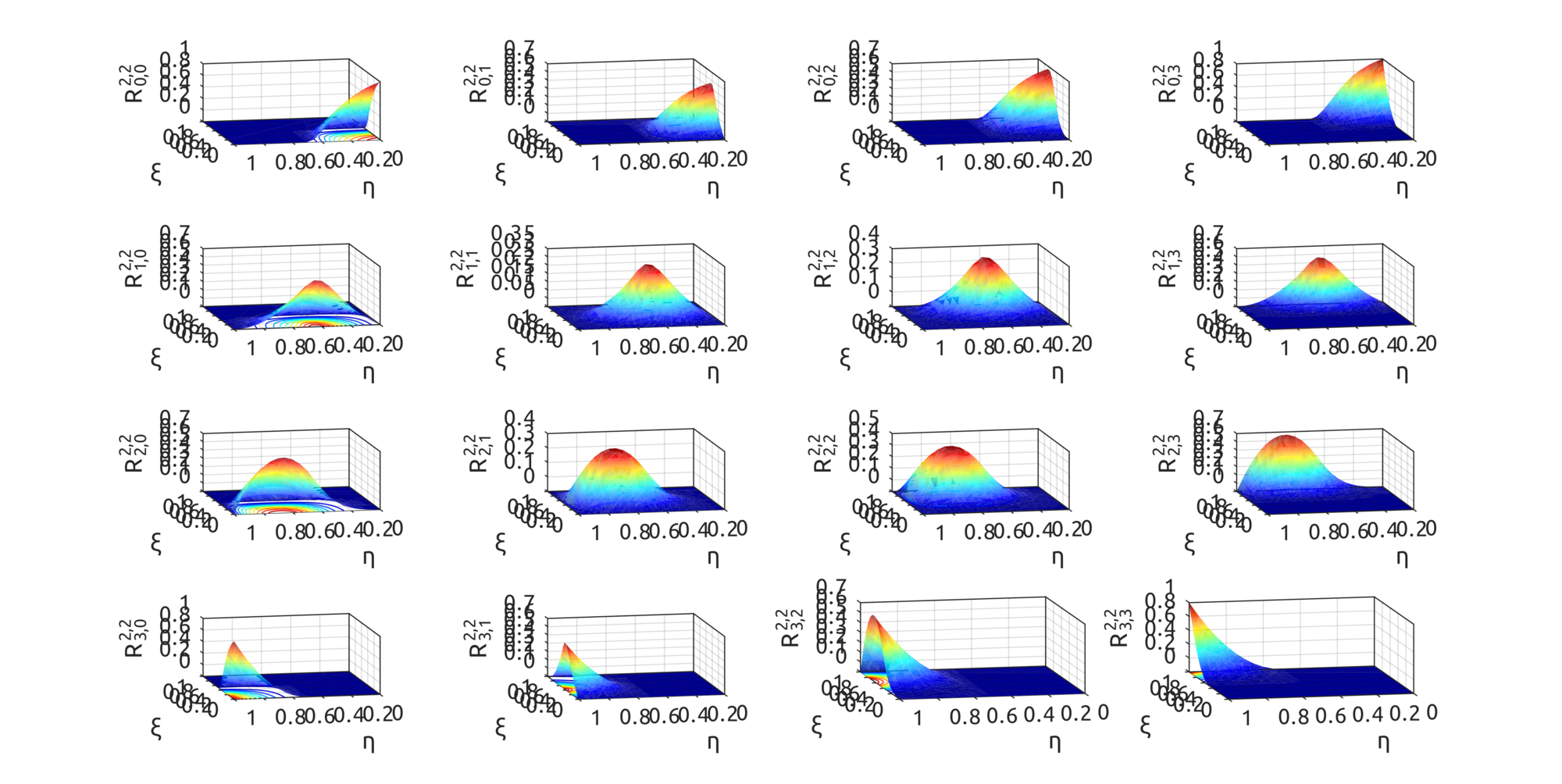
For NURBS surfaces instead we can draw bivariate basis functions. In these two examples, the first shows what happens when weights are all equal to 1, the second when weights are not all equal:
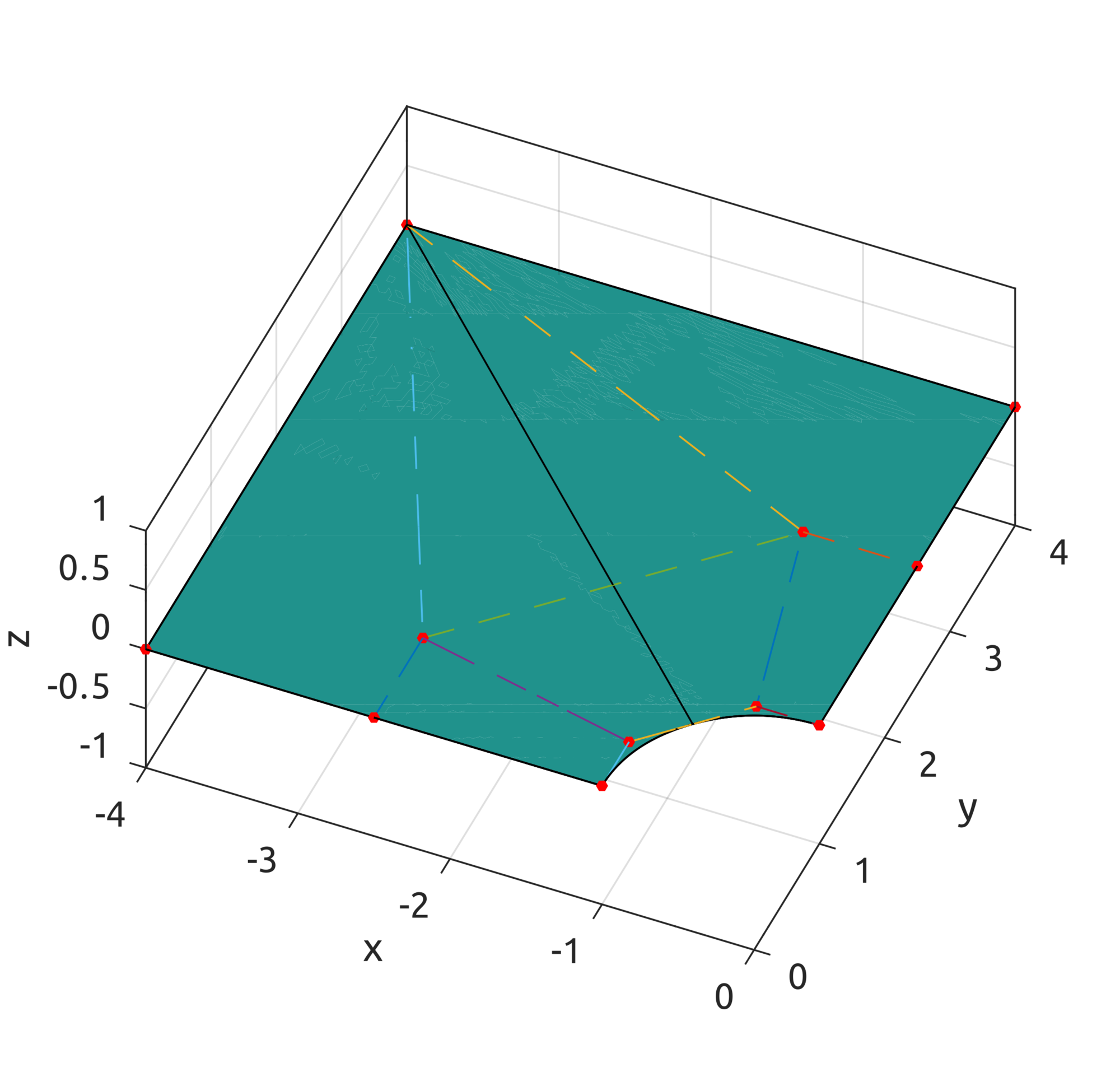
Now with the computeNURBSSurfPoint, using homogeneous coords, we can draw some interesting surfaces. Scripts are included to draw a plate with a hole:
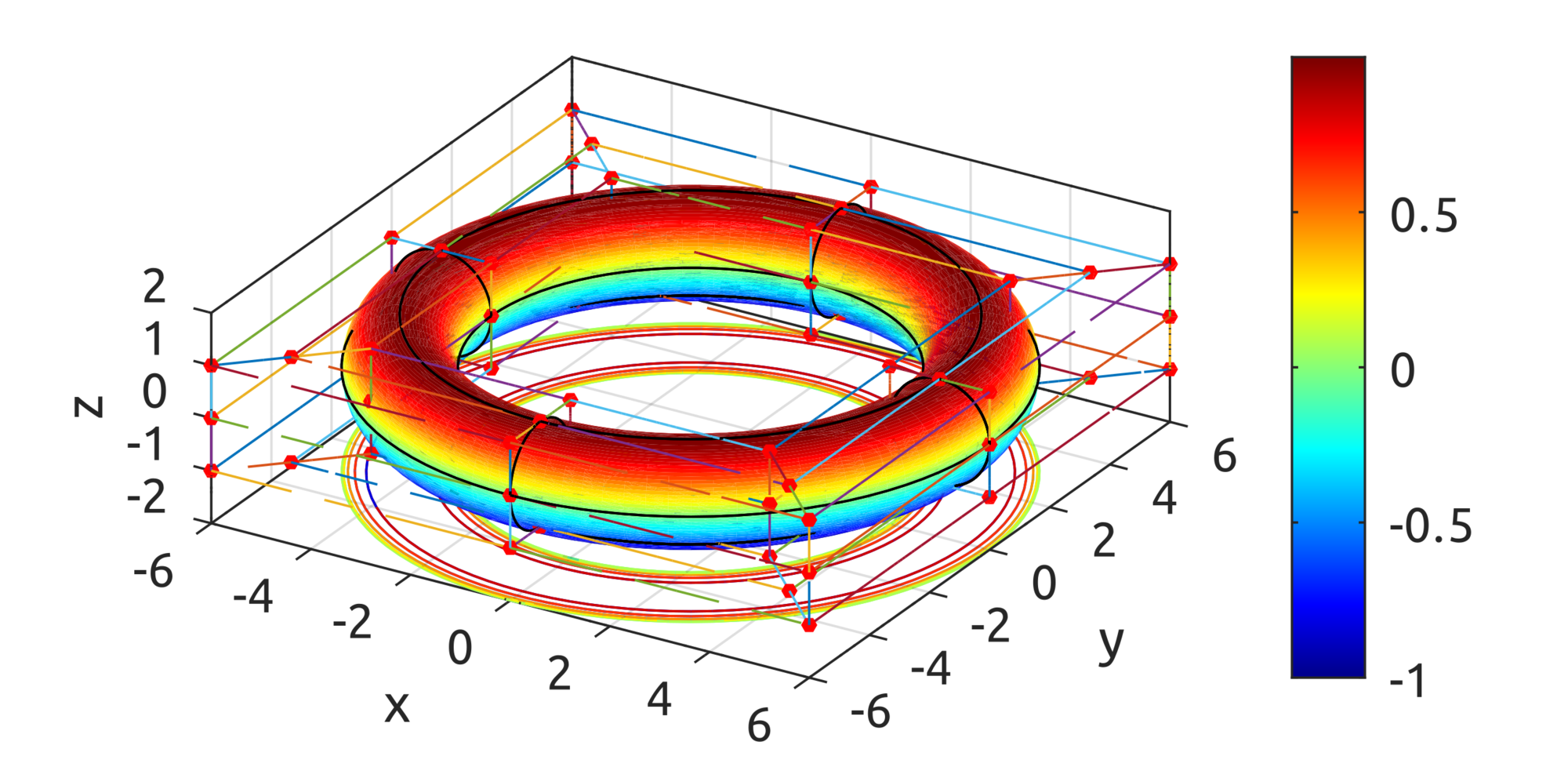
and one is provided to draw a toroid:
and you can draw the actual curves:
With the NurbsSurf class instead, you can draw the surfaces:
NURBS curves
NURBS is a generalization of B-splines where basis functions are defined with piecewise-rational polynomials. Again the parametric domain is split into multiple ranges by using a knot vector. The general definition is:
$$\displaylines{\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}R_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\\
a\leq\xi\leq b}$$
$\boldsymbol{P}_{i}$ are the control points and the functions $R_{i}^{p}$ are the NURBS basis functions, defined as:
$$\displaylines{R_{i}^{p}\left(\xi\right)=\dfrac{N_{i}^{p}\left(\xi\right)w_{i}}{{\displaystyle\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}},\\
a\leq\xi\leq b}$$
where the functions $N_i^{p}$ are the B-spline basis functions (defined here):
$$\displaylines{N_{i}^{0}\left(\xi\right)=\left\{ \begin{array}{ll}1,\xi_{i}\leq\xi<\xi_{i+1}\\0,\text{otherwise}\end{array}\right.,\\
N_{i}^{p}\left(\xi\right)=\frac{\xi-\xi_{i}}{\xi_{i+p}-\xi_{i}}\cdot N_{i}^{p-1}\left(\xi\right)+\frac{\xi_{i+p+1}-\xi}{\xi_{i+p+1}-\xi_{i+1}}\cdot N_{i+1}^{p-1}\left(\xi\right),\\
a\leq\xi\leq b}$$
and the values $w_i$’s are known as weights. The knot vector has the same definition given for B-spline curves:
$$\displaylines{\Xi=\left[\underset{p+1}{\underbrace{a,\ldots,a}},\xi_{p+1},\ldots\xi_{n},\underset{p+1}{\underbrace{b,\ldots,b}}\right],\\
\left|\Xi\right|=n+p+2}$$
NURBS surfaces
By using the tensor product we can obtain definitions for NURBS in spaces of higher dimension. For surfaces, given the knot vectors:
$$\displaylines{\Xi=\left[\underset{p+1}{\underbrace{a_{0},\ldots,a_{0}}},\xi_{p+1},\ldots,\xi_{n},\underset{p+1}{\underbrace{b_{0},\ldots,b_{0}}}\right],\\
\left|\Xi\right|=n+p+2\\
H=\left[\underset{q+1}{\underbrace{a_{1},\ldots,a_{1}}},\xi_{q+1},\ldots,\xi_{m},\underset{q+1}{\underbrace{b_{1},\ldots,b_{1}}}\right],\\
\left|H\right|=m+q+2}$$
a NURBS surface can be defined as:
$$\displaylines{\boldsymbol{S}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}R_{i,j}^{p,q}\left(\xi,\eta\right)\boldsymbol{P}_{i,j},\\
\left\{ \begin{array}{c}a_{0}\leq\xi\leq b_{0}\\a_{1}\leq\eta\leq b_{1}\end{array}\right.}$$
where:
$$\displaylines{R_{i,j}^{p,q}\left(\xi,\eta\right)=\dfrac{N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)w_{i,j}}{{\displaystyle \sum_{\hat{i}=0}^{n}\sum_{\hat{j}=0}^{m}N_{\hat{i}}^{p}\left(\xi\right)N_{\hat{j}}^{q}\left(\eta\right)w_{\hat{i},\hat{j}}}},\\
\left\{ \begin{array}{c}a_{0}\leq\xi\leq b_{0}\\a_{1}\leq\eta\leq b_{1}\end{array}\right.}$$
and $w_{i,j}$ is the weight.
Homogeneous Coordinates
The implementations found in the repo do not directly implement the summations above, but use instead homogeneous coords to make calculations simpler. Let’s consider the general form of a B-spline curve:
$$\displaylines{\boldsymbol{C}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i},\\
a\leq\xi\leq b}$$
Control points $\boldsymbol{P}_i$ can be written in homogeneous coords like this:
$$\boldsymbol{P}_{i}^{w}=\left[\begin{array}{c}
x_{i}\\
y_{i}\\
z_{i}\\
1
\end{array}\right]$$
We can multiply each control point by a value $w_i\neq 0$, and the result would still represent the same point in the euclidean space. As a result, we can write:
$$\displaylines{\boldsymbol{C}^{w}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\cdot\left[\begin{array}{c}
x_{i}w_{i}\\
y_{i}w_{i}\\
z_{i}w_{i}\\
w_{i}
\end{array}\right]=\left[\begin{array}{c}
\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)x_{i}w_{i}\\
\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)y_{i}w_{i}\\
\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)z_{i}w_{i}\\
\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}
\end{array}\right]}$$
$\boldsymbol{C}^w(\xi)$ is therefore the original B-spline curve in homogeneous coords. Now we can map back it to the euclidean space:
$$\displaylines{\boldsymbol{C}\left(\xi\right)=\left[\begin{array}{c}
\frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)x_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\
\frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)y_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\
\frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)z_{i}w_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}\\
1
\end{array}\right]}$$
which yields:
$$\boldsymbol{C}\left(\xi\right)=\frac{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}\boldsymbol{P}_{i}}{\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)w_{i}}$$
This means that, moving to homogeneous coords, we can use a simpler form. Given:
$$\boldsymbol{P}_{i}^{w}=\left[\begin{array}{c}
x_{i}w_{i}\\
y_{i}w_{i}\\
z_{i}w_{i}\\
w_{i}
\end{array}\right]$$
we can write a NURBS curve as:
$$\boldsymbol{C}^{w}\left(\xi\right)=\sum_{i=0}^{n}N_{i}^{p}\left(\xi\right)\boldsymbol{P}_{i}^{w}$$
and a NURBS surface as:
$$\displaylines{\boldsymbol{S}^{w}\left(\xi,\eta\right)=\sum_{i=0}^{n}\sum_{j=0}^{m}N_{i}^{p}\left(\xi\right)N_{j}^{q}\left(\eta\right)\boldsymbol{P}_{i}^{w}}$$
All the implementations in the repo use these simpler forms.
Octave Implementation
The computeNURBSBasisFun script can be used to compute NURBS basis functions. The drawNURBSBasisFunsP5 draws:
The computeNURBSCurvePoint script uses homogeneous coords to compute a NURBS curve using B-spline basis functions. We can build curves similar to what we could draw with B-splines but we can also draw circles:
TypeScript Implementation
The same implementation is provided for TypeScript, so you can experiment with the browser. With the NurbsCurve you can compute NURBS basis functions:Related Post
